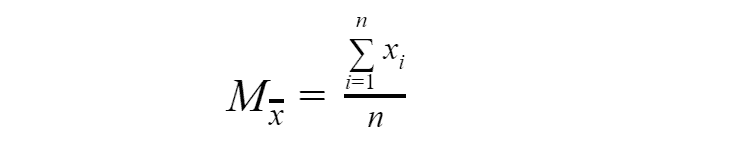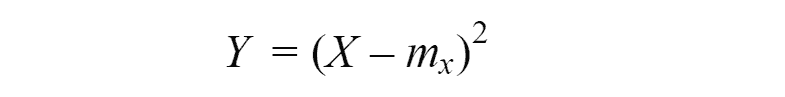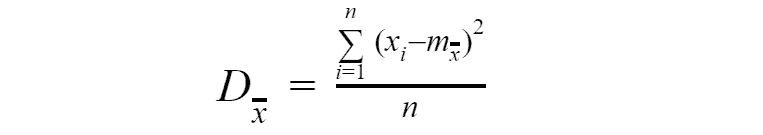Numerical Characteristics for Statistical Distribution with Python

In the previous articles, we figure out what are the numerical characteristics of random variables: expected value, variance, initial and central moments. For each such characteristic of a random variable exists statistical analog. Let’s start with an expected value.

As you can see the expected value(or statistical mean) is simply average of observations results. According to the law of large numbers, with an increase in the number of trials, the expected value converges in probability to an expected value of the random variable. With a limited number of experiments, the statistical mean is a random variable, which nevertheless, is related to the expected value and can give a representation of it. Similar statistical analogies exist for all numerical characteristics. Consider, for example, the variance of a random variable. As we remember it is an expected value of a random variable.

In order to calculate variance we applying the same formula as for random variable variance, the only change is that now will be used the different formula for calculating expected value.

The statistical initial and central moments of any orders are defined similarly. All these characteristics are completely analogous to the numerical characteristics of a random variable, with the difference that in them instead of expected value used the statistical mean. With an increase in the number of observations, it is obvious that all statistical characteristics will converge in probability to the corresponding characteristics of a separately taken random variable, and wit sufficiently large n they can be taken approximately equal to them.