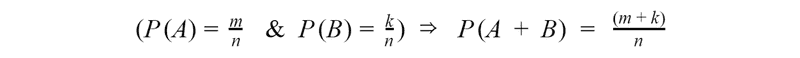Operations on Events with Python

When we determine probabilities, it is often necessary to represent complex events in the form of combinations of simpler events, applying both the addition operation and the operation of multiplying events.

Sum of two events A and B will be event C, which consists of the execution of A or B or both A and B. For example if event A is hitting of the target with the first shot and B with the second, C = A + B will be hit the target in general.

The theorem of sum looks like this: P(A + B) = P(A) + P(B). And this theorem is easy to prove:

def sum_of_probabilities(*events):
    return sum(events)

sum_of_probabilities(0.1, 0.2, 0.3)
# 0.6

Product of A and B will be event C, which consists of execution of both A and B. For example if B1 — miss at the first shot, B2 — miss at the second shot and B3 — miss at the third shot, event B= B1B2B3, mean there will not be a single hit on the target.

Before formulating product theorem we should separate events into two groups — dependent and independent events.

Event A is **independent **if P(A) independent of the occurrence of event B. For example, if you rolling dices one after another previous result will not affect the next experiment.

Event A depends on event B if P(A) will change if B occurs or not. The probability of event A, in case of occurrence of event B, is conditional probability — P(A|B). For example, after each time you take the card from the desk, it will affect the probability of taking a specific card next time.

The probability of the product of two events is equal to the product of the probabilities of one of them by the conditional probability of the other, calculated on the condition that the former took place.

P(AB) = P(A) P(B|A)