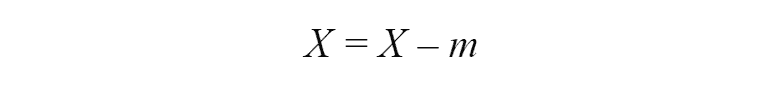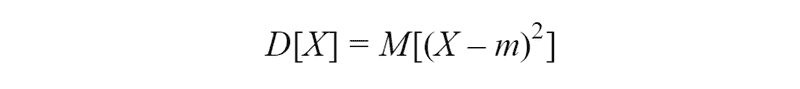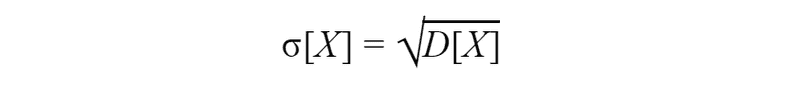Moments, Variance, Standard Deviation With Python

In the previous post, we had a look at characteristics, that shows the position of a random variable on the numerical axis. But there is also a number of characteristics which describe certain distribution properties — Moments. Most of the time we will deal with two types of moments — initial and central.

The initial moment of the s-th order of a discrete random variable X is a sum of the form:

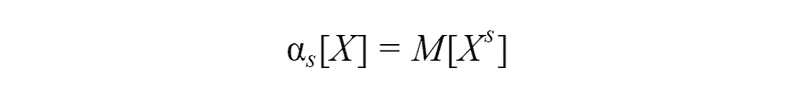
For continuous random variable we have:

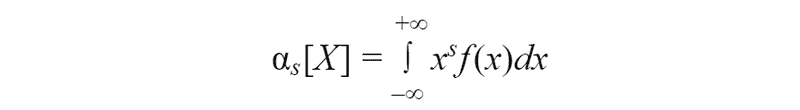
As you can see that the first initial moment is expected value. Also for the initial moment, we can join two previous formulas in one.

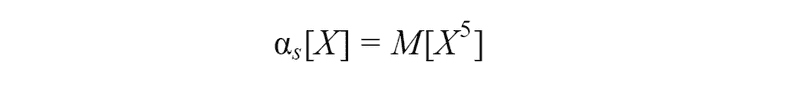
Let’s see how distribution function will change according to the expected value.

Before we approach central moment we introduce the central random variable. For random variable X with expected value m. Central random variable is deviation of a random variable from its expected value:

Thus, the central moment of the s-th random variable *X *is the expected value of the s-th degree of the corresponding central random variable. For a discrete random variable:

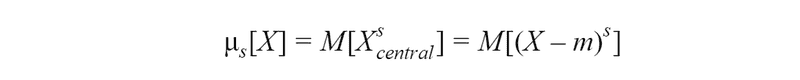
And for continuous random variable:

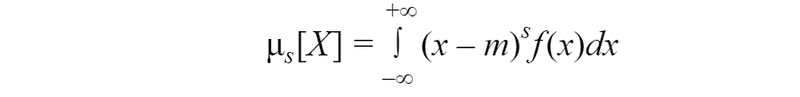
A very important characteristic is the second central moment — Variance. Varianceis characteristic of dispersion, scatter of values of a random variable near its expected value.

Let’s see how distribution function will change according to the expected value.

For a visual characteristic of dispersion, it is more convenient to use a quantity whose dimension coincides with the dimension of the random variable. To do this, a square root is extracted from the dispersion. The value obtained is called the standard deviation. In practice, you will see a standard deviation more often then variance.

from math import sqrt

def expected_value(values, probabilities):
    return sum([v * p for v, p in zip(values, probabilities)])

def standard_deviation(values, probabilities):
    m = expected_value(values, probabilities)
    return sqrt(sum([(v - m)**2 * p for v, p in zip(values, probabilities)]))

values = [1, 2, 5, 3, 8, 4]
probabilities = [.1, .2, .4, .1, .15, .05]

standard_deviation(values, probabilities)
# 2.1354

Expected value, variance and standard deviation — the most commonly used characteristics of a random variable. They characterize the most important features of the distribution: its position and degree of dispersion. For a more detailed description of the distribution, higher-order moments are used. But they are out of the scope of this article.