Central Limit Theorem with Python

The central limit theorem tells us that the sample mean will be approximately normally distributed for large sample sizes, regardless of the distribution from which we are sampling. Suppose we are sampling from a population with mean μ and standard deviation σ. Let Y be a random variable representing the sample mean for n independently drawn observations. The mean of the sampling distribution of the sample mean is equal to the population mean. And the standard deviation of the sampling distribution of Y is equal to:

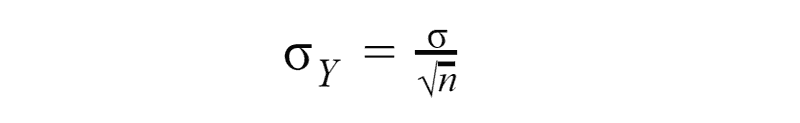
If the population is normally distributed, then Y is also normally distributed. And if the population is not normal we can use the central limit theorem — the distribution of the sample mean tends toward the normal distribution as the sample size increases, regardless of the distribution from which we are sampling.

Let’s take the population with the logarithmic distribution. And make four experiments. The first time we will take two random values from a population million times and calculate mean, the second time we will take four and last time we will take 10. From charts, you will see that by increasing the number of samples distribution of means looks more like the normal distribution.

And let’s also try uniform distribution.

As you can see no matter what the distribution population has when we take a large sample of the population we have normally distributed means.

Many statistics have distributions that are approximately normal for large sample sizes, even when we are sampling from a distribution that is not normal. It means that we can use normal distribution tools even if we are sampling from a population that is not normal, provided we have a large sample size.

An example of such a situation will be a task where you need to find the probability that the average of a randomly selected sample will be larger or less than some value. In order to solve such a task, you need to have a mean and standard deviation of the population only.