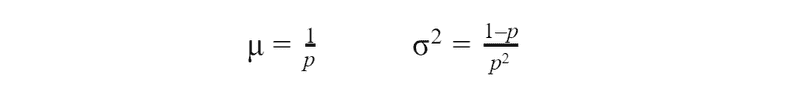Geometric Distribution With Python

This is the first part of a series of articles about different types of distributions. There is a lot of different distributions out there, but we will cover the most popular ones, those more often used to be approximate versions of real data.

The geometric distribution is the distribution of the number of trials needed to get the first success in repeated Bernoulli trials. Repeated Bernoulli trials mean that all trials are independent and each result have two possible outcomes. Random variable *X *represents the number of trials needed to get the first success. In order to the first success occur on the xth trial the first *x-1 *trials must be failures and the xth trial must be a success. The value x can be any integer from 0, it doesn’t have an upper bound.

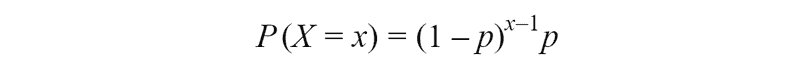
Let’s take a look at the example. Imagine that we have the event with probability to occur equal to* 0.2*. What is the probability that this event occurs on the third attempt?

As you can see from the bar chart the minimum value of the attempt is 1 and there is no maximum value.

Let’s take a look at the characteristics of the geometric distribution. The mean and the variance:

There is also some interesting properties of the geometric distribution. Let’s find the probability that event occurs before the fourth attempt:

def probability_that_event_occur_before(attempt, probability):
    return 1 - (1 - probability)**(attempt - 1)

p = 0.2
probability_that_event_occur_before(4, p)
# 0.488