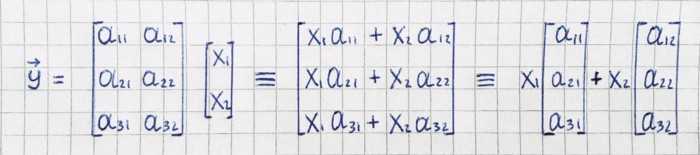Linear Transformation and Matrix With JavaScript

A matrix is a rectangular array of real numbers with m rows and n columns. For example, a 3×2 matrix looks like this:

Let’s go right to the code. The constructor of the Matrix class will receive rows as a parameter. We will access a particular element in the matrix by first taking row by row index and then element by column index.

class Matrix {
  constructor(...rows) {
    this.rows = rows
  }
}

const matrix = new Matrix(
  [0, 1],
  [2, 3],
  [4, 5]
)
console.log(matrix)
// Matrix { rows: [ [ 0, 1 ], [ 2, 3 ], [ 4, 5 ] ] }
console.log(matrix.rows[1])
// [ 2, 3 ]
console.log(matrix.rows[1][1])
// 3

Matrix-vector product

The matrix-vector product Ax⃗ produces a linear combination of the columns of the matrix A with coefficients x⃗. For example, the product of a 3×2 matrix A and a 2D vector *x⃗ *results in a 3D vector, which we’ll denote y⃗: y⃗=Ax⃗

Consider some set of vectors {e⃗₁, e⃗₂}, and a third vector y⃗ that is a linear combination of the vectors e⃗₁ and e⃗₂: y⃗=αe⃗₁ + βe⃗₂. The numbers α, β ∈ R are the coefficients in this linear combination.

The matrix-vector product is defined expressly for the purpose of studying linear combinations. We can describe the above linear combination as the following matrix vector product: y⃗=Ex⃗. The matrix E has e⃗₁ and e⃗₂ as columns. The dimensions of the matrix will be n×2, where n is the dimension of the vectors e⃗₁, e⃗₂ and y⃗.

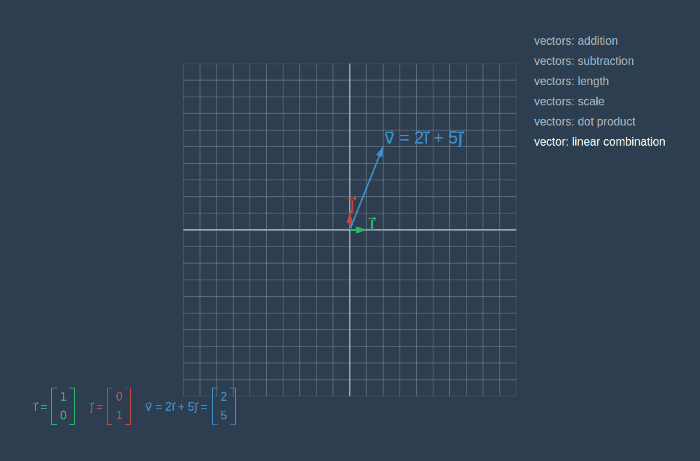
In the picture below we can see vector v⃗ represented as a linear combination of vectors* î* and ĵ.

const i = new Vector(1, 0)
const j = new Vector(0, 1)
const firstCoeff = 2
const secondCoeff = 5
const linearCombination = i.scaleBy(firstCoeff).add(j.scaleBy(secondCoeff))
console.log(linearCombination)
// Vector { components: [ 2, 5 ] }

Linear Transformation

The matrix-vector product corresponds to the abstract notion of a linear transformation, which is one of the key notions in the study of linear algebra. Multiplication by a matrix can be thought of as computing a linear transformation that takes n-dimensional vector as an input and produces m-dimensional vector as an output. We can say matrix is a certain transformation of vector in space.

It will become more clear on examples, but first, let’s add a method to Matrix class that will return columns of the matrix.

class Matrix {
  constructor(...rows) {
    this.rows = rows
  }
  columns() {
    return this.rows[0].map((_, i) => this.rows.map(r => r[i]))
  }
}

const matrix = new Matrix(
  [1, 2, 3],
  [4, 5, 6],
  [7, 8, 9]
)
console.log(matrix.columns())
// [ [ 1, 4, 7 ], [ 2, 5, 8 ], [ 3, 6, 9 ] ]

In the code sample below you can examples of different vector-matrix products. The dimension of the resulting vector will always be equal to the number of matrix rows. If we multiply a 2D vector to a 3×2 matrix, we will receive a 3D vector, and when we multiply a 3D vector to a 2×3 matrix, we will receive a 2D vector. If a number of columns in the matrix not equal to vector dimension, we throw an error.

const sum = arr => arr.reduce((acc, value) => acc + value, 0)

class Vector {
  // ...
  transform(matrix) {
    const columns = matrix.columns()
    if(columns.length !== this.components.length) {
      throw new Error('Matrix columns length should be equal to vector components length.')
    }

    const multiplied = columns
      .map((column, i) => column.map(c => c * this.components[i]))
    const newComponents = multiplied[0].map((_, i) => sum(multiplied.map(column => column[i])))
    return new Vector(...newComponents)
  }
}

const vector2D = new Vector(3, 5)
const vector3D = new Vector(3, 5, 2)
const matrix2x2D = new Matrix(
  [1, 2],
  [3, 4]
)
const matrix2x3D = new Matrix(
  [1, 2, 3],
  [4, 5, 6]
)
const matrix3x2D = new Matrix(
  [1, 2],
  [3, 4],
  [5, 6]
)

// 2D => 2D
console.log(vector2D.transform(matrix2x2D))
// Vector { components: [ 13, 29 ] }

// 3D => 2D
console.log(vector3D.transform(matrix2x3D))
// Vector { components: [ 19, 49 ] }

// 2D => 3D
console.log(vector2D.transform(matrix3x2D))
// Vector { components: [ 13, 29, 45 ] }
console.log(vector2D.transform(matrix2x3D))
// Error: Matrix columns length should be equal to vector components length.

Examples

Now let’s try to move and change the two-dimensional object by using linear transformations. First, we will create a new class — Contour that will receive a list of vectors in the constructor and for now, will have only one method — transform, that will transform all coordinates of the contour and will return a new one.

class Contour {
  constructor(vectors) {
    this.vectors = vectors
  }

  transform(matrix) {
    const newVectors = this.vectors.map(v => v.transform(matrix))
    return new Contour(newVectors)
  }
}

const contour = new Contour([
  new Vector(0, 0),
  new Vector(0, 4),
  new Vector(4, 4),
  new Vector(4, 0)
])

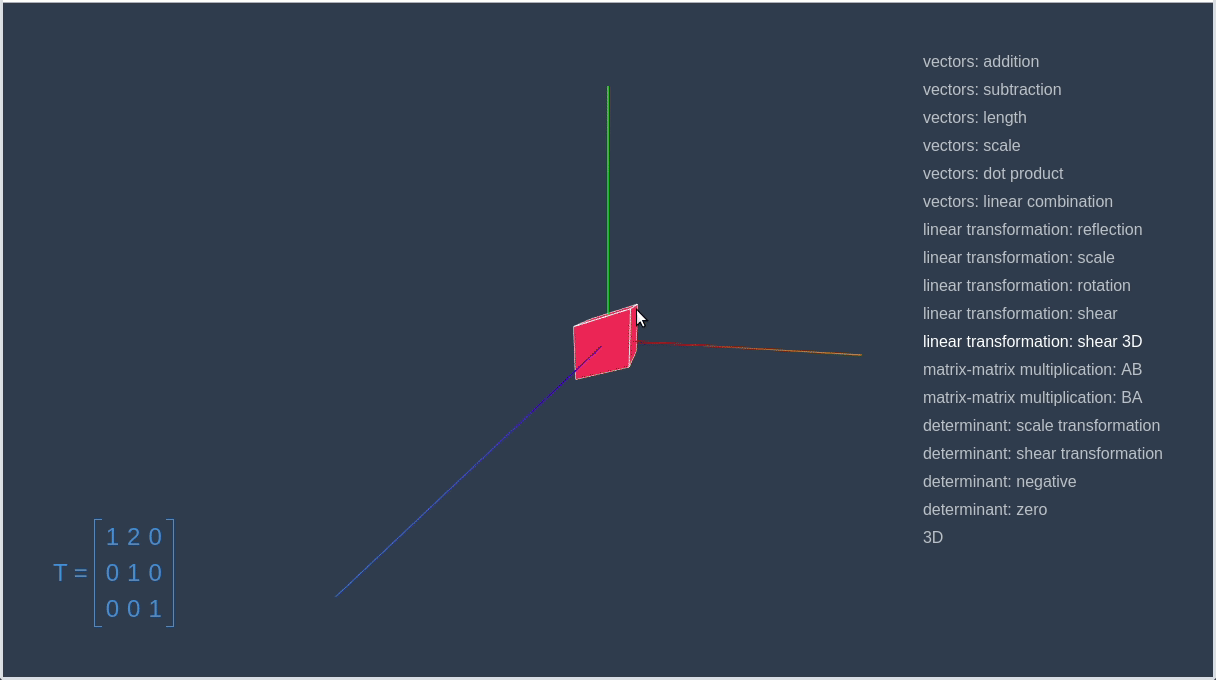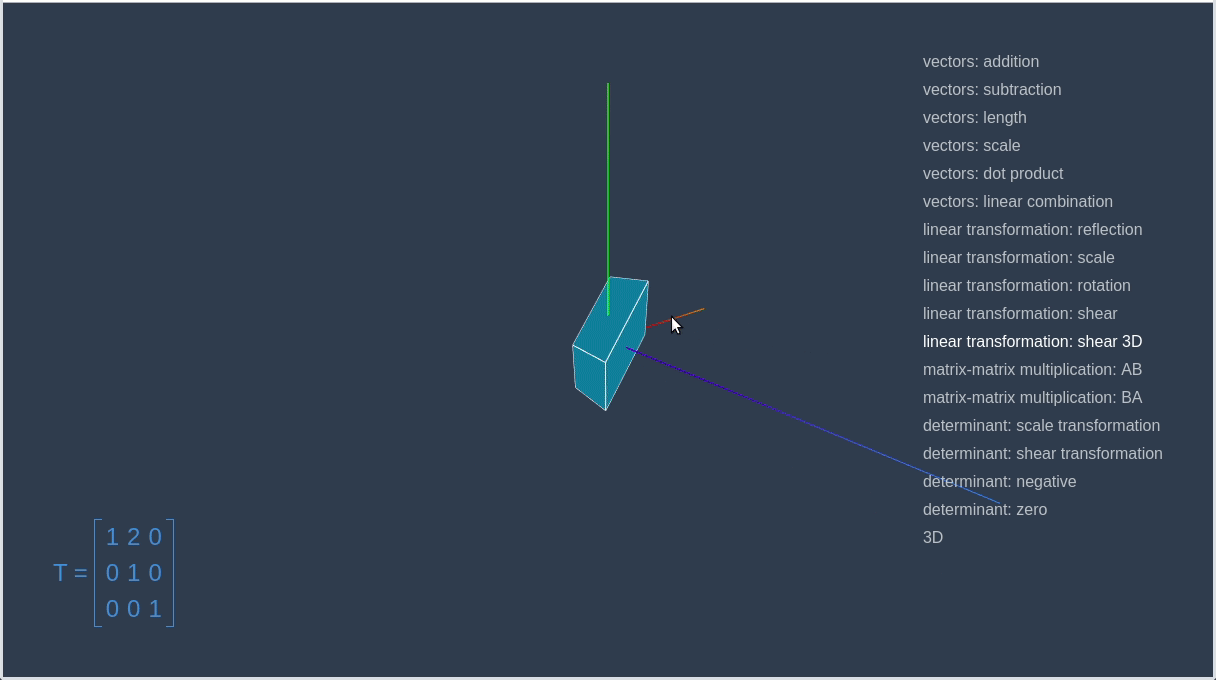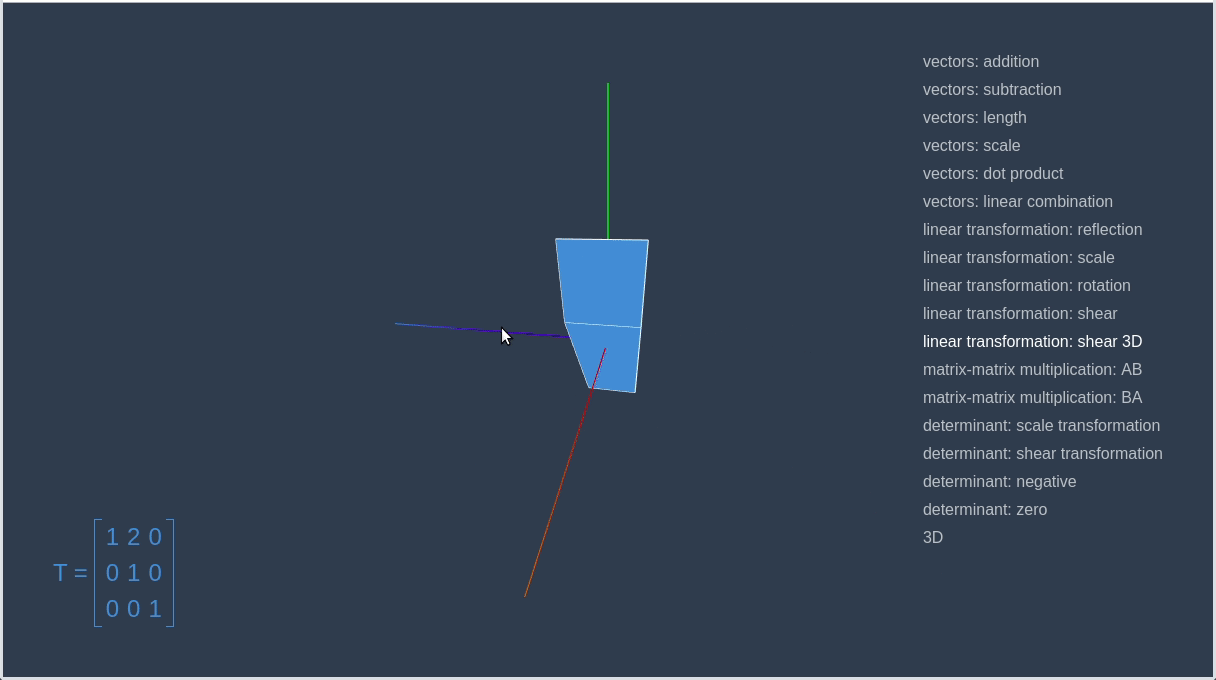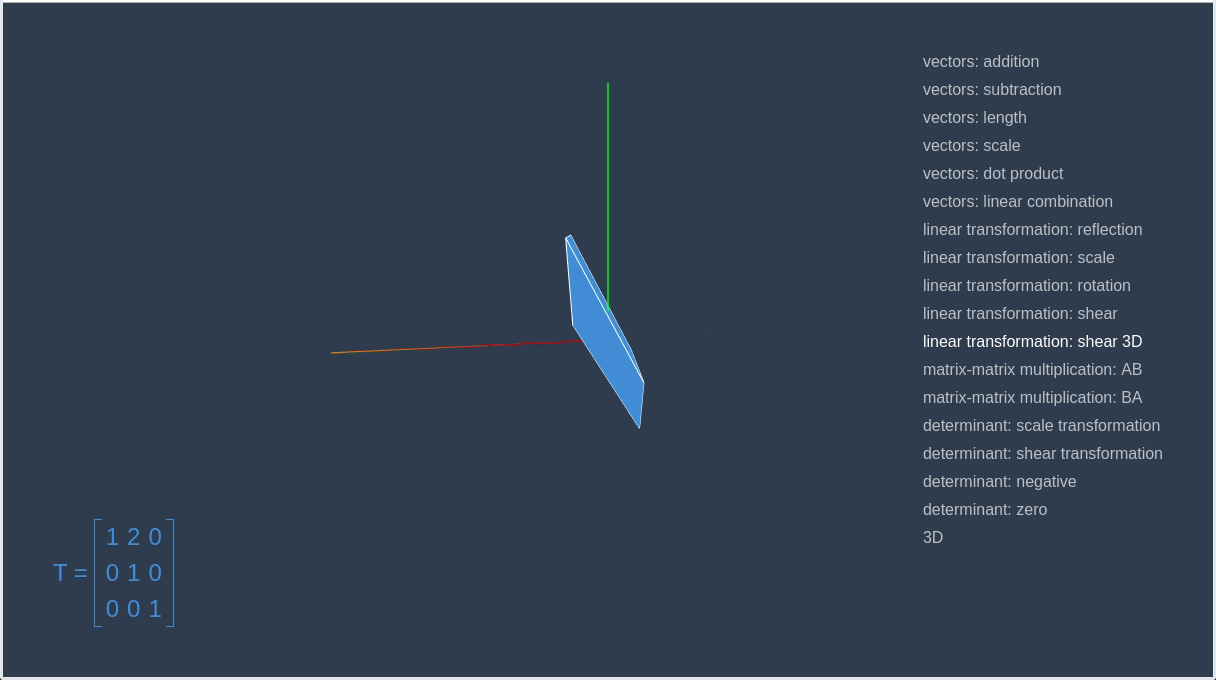
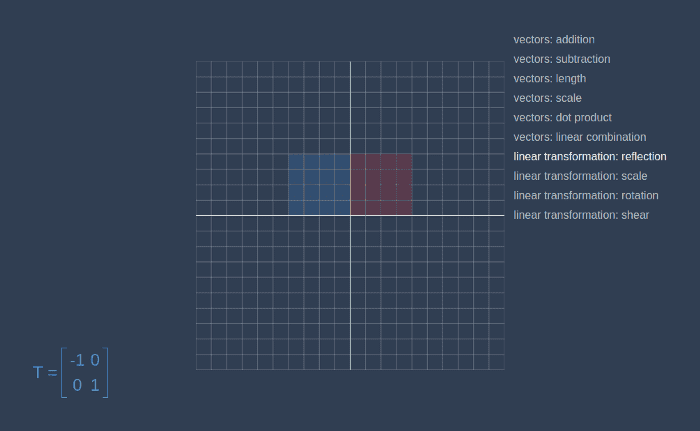
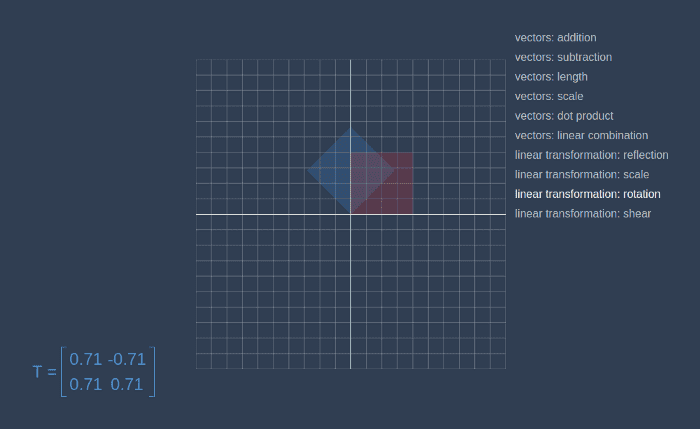
Now, let’s go to the linear-algebra-demo project and try out different transformation matrices. Red square is an initial contour, and the blue one is a result of applying the transformation.

This way we can make a matrix that will rotate a given vector on a certain angle.

const angle = toRadians(45)

const matrix = new Matrix(
  [Math.cos(angle), -Math.sin(angle)],
  [Math.sin(angle), Math.cos(angle)]
)

Transformation works the same way for objects in 3D space, below you can see the animated transformation from the red cube, to blue parallelepiped.